Aktualnie montowane statyczne liczniki energii elektrycznej przez operatorów systemu dystrybucyjnego oparte są na konwersji analogowo-cyfrowej sygnałów prądowych i napięciowych, zastępują tradycyjne liczniki indukcyjne. Dodatkową zaletą liczników statycznych są wielofunkcyjne udogodnienia takie jak możliwość przesyłania danych pomiarowych, pomiar energii czynnej i biernej, pomiar mocy.
Podstawową zasadą mierników statycznych jest zastosowanie odpowiednich wzorów matematycznych i algorytmów uwzględniających zawartość harmonicznych napięcia i prądu.
Normy EN50160 [7] i IEC-61000-4-30 [8] regulujące dokładność i niezawodność liczników energii elektrycznej definiują wymagania jakie muszą być spełnione w warunkach sinusoidalnych.
Normy określają także przeprowadzenie uśredniania wyznaczonych wartości Ah w bardzo krótkim (3 s), krótkim (10 min.) i długim (2 godz.) czasie pomiaru. Podstawowymi wyznacznikami cyfrowego przetwarzania sygnałów i zaburzeń okresowych są stosowane algorytmy zależne od:
- Rozdzielczości przetwornika analogowo – cyfrowego.
- Rozdzielczości analizy DFT.
- Liczby przetwarzanych próbek.
- Rodzaju próbkowania (synchroniczne lub asynchroniczne).
Powyższe uwarunkowania mają dojmujący wpływ na niepewność wyznaczania wskaźnika THD. W przypadku nieuwzględniania w obserwowanym przebiegu napięcia zaburzeń okresowych sprzężonych z częstotliwością podstawową sieci prowadzi to do błędów wyznaczania wartości współczynnika zawartości harmonicznych zgodnie z podanym wcześniej wzorem.
W przypadku wystąpienia zniekształceń harmonicznych pogarsza się charakterystyka metrologiczna układu pomiarowego co może prowadzić do utraty niezawodności specyfikacji określanych w warunkach sinusoidalnych. Nie ma wątpliwości że szczególnie w systemach niskiego napięcia liczniki powinny być też certyfikowane przy przebiegach odkształconych.
Dotychczasowa technika która pozwala na pomiar mocy z zawartością składowych wyższych harmonicznych opiera się na założeniu że zarówno przebieg prądu jak i napięcia można rozłożyć w szereg Fouriera i w tym przypadku moc jest równa sumie mocy poszczególnych składowych.
Przyczyny powstawania tych składowych to między innymi szybkie zmiany obciążenia odbiorników dużej mocy np. pieców indukcyjnych (rys. 1), urządzeń walcowniczych jak również coraz liczniejsza grupa urządzeń małej mocy falowniki, inwertery w źródłach energii typu elektrownia wiatrowa czy fotowoltaiczna mogą powodować wahania napięcia które są w istocie nałożeniem subharmonicznych i interharmonicznych co powoduje często nieprawidłową pracę urządzeń pomiarowych mających dosyć ograniczone możliwości obliczeniowe oparte na zaimplementowanej sprzętowej transformacie Fouriera.
W przypadku wystąpienia subharmonicznych i interharmonicznych przebiegi prądu i napięcia przestają być okresowe. Fakt ten eliminuje możliwość analizy w oparciu o rozkład szeregu Fouriera [4]. Z tego też powodu niezwykle istotne jest określenie poziomu zawartości subharmonicznych i interharmonicznych, które nie powodują powstania błędu pomiaru przekraczającego dopuszczalną zakładaną wartość i dokładność pomiaru [4]. W przypadku znacznej zawartości składowych subharmonicznych i interharmonicznych konieczne jest opracowanie nowego podejścia do pomiaru mocy czynnej.
Analizowane były przypadki zastosowania szeregu Prony’ego do tych celów. Jednak w takich sytuacjach wymagana jest duża moc obliczeniowa układu analizującego co eliminuje możliwość zastosowania tych szeregów w masowo instalowanych licznikach pomiaru energii elektrycznej.

1. Przebiegi odkształcone ze składową podstawową i zawartością wyższych harmonicznych.
W odróżnieniu od przebiegów sinusoidalnych, przy przebiegach odkształconych, suma kwadratów mocy czynnej i mocy biernej nie jest równa kwadratowi mocy pozornej.
Zgodnie z twierdzeniem Fouriera dowolny przebieg okresowy można opisać poprzez sumę składników:
- Składowa sinusoidalna o częstotliwości podstawowej (harmoniczna podstawowa, składowa podstawowa).
- Składowe sinusoidalne o częstotliwościach będących wielokrotnościami częstotliwości podstawowej (wyższe harmoniczne).
- Każdy przebieg odkształcony napięcia lub prądu może być utworzony z harmonicznych tak też każdy przebieg okresowy może być poddany rozkładowi na harmoniczne.
Odkształcenie przebiegów prądu i napięcia może być scharakteryzowane w czasie lub częstotliwości, przebieg w dziedzinie czasu charakteryzuje się na określeniu różnic pomiędzy wartościami rzeczywistego odkształconego przebiegu a wartościami wzorcowego przebiegu sinusoidalnego. Natomiast przebieg w dziedzinie częstotliwości dostarcza zbiór liczb określających rzędy, amplitudy (wartości skuteczne) i fazy poszczególnych harmonicznych. Dokonanie analizy obwodów, w których wartości elektryczne (prąd, napięcie) nie są sinusoidalnie zmienne jest dosyć trudne.
Stosujemy matematyczne przekształcenie polegające na tym, że daną funkcję niesinusoidalną zastępuje się szeregiem trygonometrycznym Fouriera, który jest nieskończoną sumą składowych przebiegów sinusoidalnych, ale o różnych amplitudach i coraz wyższych częstotliwościach (1).
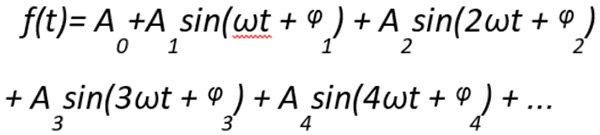
Moc czynna w przebiegach odkształconych jest równa sumie mocy czynnych poszczególnych harmonicznych oraz mocy składowej stałej i jej definicja przy obecności harmonicznych to:
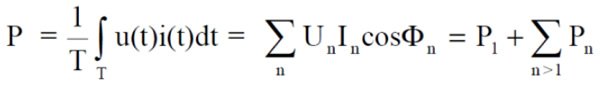
Dodatkowe błędy aktywnych mierników mocy spowodowane przez harmoniczne będą powodowane głównie przez ograniczenia pasma przenoszenia, zwłaszcza dla starszych mierników analogowych. Ponieważ zakłada się, że podstawowy kąt fazowy wynosi zero w naszym przykładzie, a wszystkie inne kąty są π, moc czynna będzie:
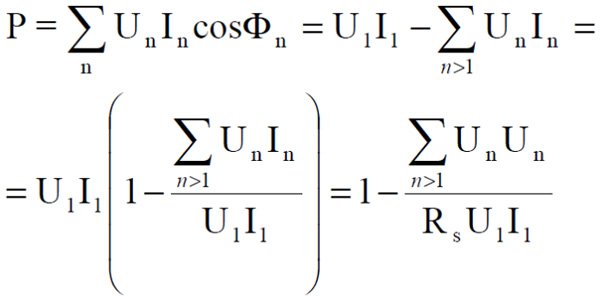
Gdzie: Rs jest całkowitą impedancją źródła, ponieważ przyjmuje się, że Φ1 równa się 0. Rs jest wtedy przyjmowane jako niezależne od częstotliwości, a zatem może być obliczane z THD jako:
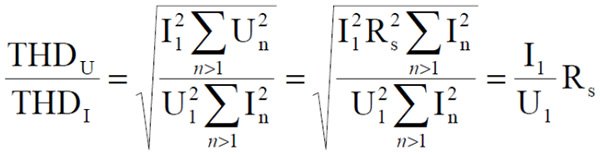
Biorąc pod uwagę przedstawione zależności można obliczyć moc czynną:
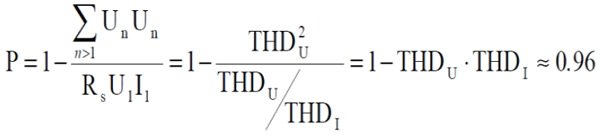
Oznacza to, że całkowita moc czynna P jest maksymalnie około 4% mniejsza niż podstawowa moc czynna P1. W związku z tym błąd miernika o bardzo ograniczonej szerokości pasma wynosiłby w tej sytuacji około 4%.
Moc bierna przy przebiegach odkształconych jest równa sumie mocy biernych poszczególnych harmonicznych, czyli przy n harmonicznych ma postać:
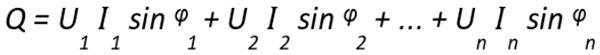

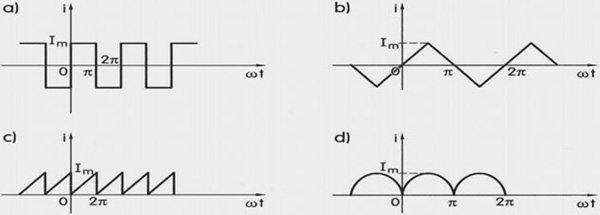
Przykłady rozwinięć szeregu Fouriera dla wybranych przebiegów prądów niesinusoidalnych:
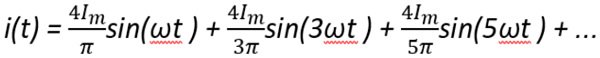
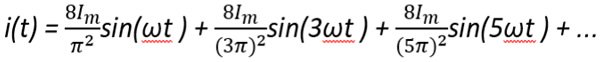
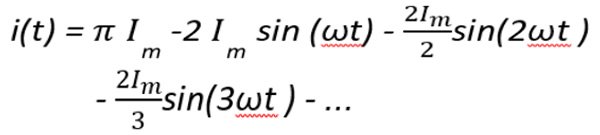
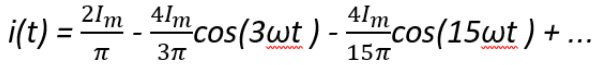
Dokładne pomiary niesinusoidalnych sygnałów elektrycznych mogą być dokonywane przez równoczesne pobieranie próbek napięcia i prądu w równych odstępach podczas całkowitej wielokrotności okresów częstotliwości podstawowej.
W przypadku, gdy prądy i napięcia nie są sinusoidalne, dobry opis stanu systemu zasilania wymaga oddzielenia sygnału w postaci jego składowych harmonicznych. Dotyczy to szeregu sugerowanych rozszerzeń teorii mocy w celu objęcia stanu niesinusoidalnego. W tym przypadku DFT (Dyskretna transformata Fouriera) jest skuteczną metodą obliczeniową, która umożliwia pomiary amplitud i kątów fazowych poszczególnych harmonicznych niesinusoidalnych napięć i prądów. Po ich uzyskaniu można obliczyć większość parametrów, takich jak moce i zniekształcenia harmoniczne (całkowite). Ponadto te metody obliczeniowe umożliwiają stosowanie korekcji zależnych od częstotliwości, co zwiększa również dokładność pomiarów (całkowitej) mocy czynnej sygnałów niesinusoidalnych.
Niektóre wielkości, takie jak moc bierna, nie są właściwie zdefiniowane dla sytuacji niesinusoidalnych. Ciągle są podejmowane prace w celu zrozumienia i wyjaśnienia problemów związanych z rozszerzeniem definicji mocy biernej na sytuacje niesinusoidalne. Główny wniosek jest taki, że moc bierna jest wykorzystywana do uzyskania informacji o więcej niż jednej właściwości mechanizmu przenoszenia mocy, np. kąt fazowy, wydajność transmisji i spadek napięcia linii. Nie istnieje jedna definicja, która mogłaby dostarczyć informacji o wszystkich tych właściwościach w sytuacji niesinusoidalnej. Co więcej, konstrukcja wielu instrumentów jest taka, że nie są zgodne z żadną rozszerzoną definicją pomiaru mocy. W sytuacji niesinusoidalnej liczniki będą wykazywać dodatkowe błędy z powodu tej niezgodności.
2. Błędy pomiarowe spowodowane harmonicznymi.
Całkowite zniekształcenia harmoniczne, czyli współczynnik zniekształceń (THD, d lub h), są często używane do ilościowego określania poziomu harmonicznych. Jest to dobry przykład tego, jak różne definicje mogą powodować zamieszanie i możliwe błędy. THD dla sygnału niesinusoidalnego jest zdefiniowane jako całkowita wartość skuteczna harmonicznych.
Pomiar zniekształceń harmonicznych mocy w sytuacjach niesinusoidalnych można obliczać w porównaniu do wartości składowej podstawowej U1 lub w porównaniu do całkowitej wartości skutecznej Urms. Na przykład THD dla napięcia jest zdefiniowane jako:
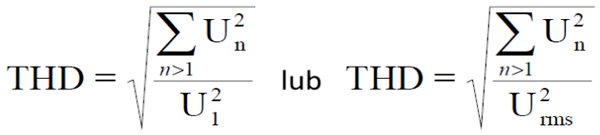
Poniżej 10% THD różnica między dwiema definicjami jest pomijalna. Pierwsza definicja wydaje się mieć coraz większe poparcie w organizacjach normalizacyjnych, ponieważ niektóre obliczenia są łatwiejsze dzięki tej definicji. Ze względów praktycznych liczba harmonicznych jest ograniczona, gdy obliczane jest THD; ten limit jest najczęściej w zakresie n = 30 do n = 40. Aby oddzielić napięcie THD od prądu THD, w tej używamy czasami skrótów THDU i THDI.
Chociaż przeprowadzono wiele badań przypadków w sytuacjach, w których wystąpiły problemy z wyższymi harmonicznymi, nie ma ogólnych zasad dotyczących tego, czego można się spodziewać w zakresie prądu i napięcia THD dla różnych odbiorników energii. Indywidualne mniejsze obciążenia jednofazowe, w tym komputery i energooszczędne lampy, mogą powodować prąd THD na poziomie około 100%, trójfazowe przetworniki o sztywnym napięciu powodują również zniekształcenia prądu na tym poziomie [5]. Trójfazowy konwerter 6-impulsowy bez filtrów spowoduje maksymalny prąd THD 20-30%. Większość sprzętu elektronicznego i oświetlenia fluorescencyjnego spowoduje prąd THD od 20% do 100%. Jednak harmoniczne prądu o różnych kątach fazowych częściowo się znoszą, nawet na poziomie pojedynczych odbiorników mocy. Tak więc, nawet jeśli całe obciążenie składa się z małych obciążeń wysokich THD to THD całkowitego prądu będzie znacznie niższe niż 100%. Ponadto aktualny poziom całkowity THD dla prądu nie osiągnie maksimum w warunkach wysokiego obciążenia, ponieważ urządzenia o niskim THD stanowią wówczas znaczną część obciążenia.
W przypadku większych obciążeń nieliniowych napięcie THD zależy głównie od połączonych skutków impedancji źródła i aktualnego poziomu THD. Napięcie THD będzie zatem często o 5 – 15 razy niższe niż obecne THD dla większych obciążeń. W przypadku mniejszych obciążeń nie ma takiej reguły, ponieważ napięcie THD będzie wtedy również zależeć od innych czynników, takich jak inne pobliskie obciążenia nieliniowe.
Rozsądnie wysokie wartości mogą wynosić 20-30% prądu THD i 3-5% napięcia THD. Dodatkowe błędy wynikające z wpływu harmonicznych na pomiary można podzielić na trzy grupy. Pierwszą grupą są częste błędy spowodowane nieliniowością na obwodzie wejściowym lub pomiarowym oraz ograniczoną odpowiedzią częstotliwościową. Druga grupa składa się z błędów systematycznych spowodowanych przez instrumenty wykorzystujące zasady pomiaru, które nie są zgodne z rozszerzonymi definicjami sytuacji niesinusoidalnych. Trzecia grupa błędów wynika z zastosowania różnych konkurencyjnych definicji niektórych wielkości, dając różne wyniki w sytuacjach niesinusoidalnych. Dodatkowo, jeśli zmierzone wielkości zostaną użyte w dalszych obliczeniach, błędy te będą miały wpływ na wyniki obliczeń w sposób określony przez algorytm obliczeniowy. Zwykle mierniki napięcia i prądu wskazują wartości średniej kwadratowej (RMS), które dla sygnału okresowego są podawane przez:
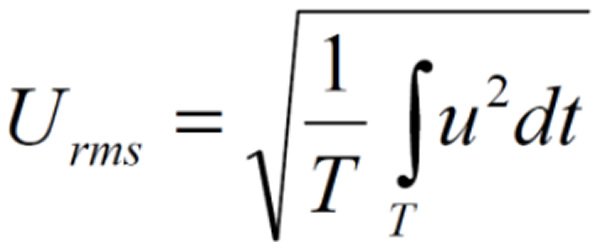
Bardzo często miernik mierzący wartość skuteczną nazywany jest licznikiem “prawdziwej wartości skutecznej”, aby oddzielić ten pomiar od innych mierników wskazujących wartości skuteczne, podczas gdy w rzeczywistości mierzy się coś innego, np. skorygowaną wartość średnią. Chociaż jest to raczej potoczne określenie, “prawdziwa wartość skuteczna” przyjęto ją dla uproszczenia. Dodatkowe błędy rzeczywistych liczników RMS z powodu harmonicznych będą powodowane głównie przez wyższe wymagania dotyczące szerokości pasma i liniowości dla sytuacji niesinusoidalnych. Powyższa definicja może być zastosowana do reprezentacji sygnału w szeregu Fouriera dla napięcia wartości skutecznej:
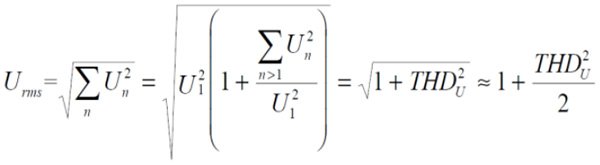
Podobnie będzie wyglądał wzór na względny prąd skuteczny:
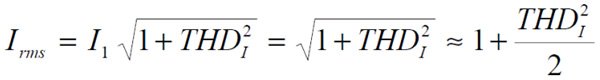
3. Przebiegi odkształcone z zawartością subharmonicznych i interharmonicznych.
Składowe subharmoniczne napięcia i prądu to niecałkowite krotności mniejsze od częstotliwości podstawowej 50Hz czyli na przykład 27Hz.
Składowe interharmoniczne to niecałkowite wielokrotności częstotliwości podstawowej 50Hz czyli np. 177Hz mogące pojawiać się jako częstotliwości dyskretne lub jako szerokopasmowe spektrum.
W przypadku analizy interharmonicznych i subharmonicznych problem prawidłowego pomiaru przez liczniki statyczne staje się trudniejszy. Częstotliwości tych składowych nie tylko nie są całkowitymi krotnościami częstotliwości podstawowej, ale dodatkowo często ulęgają zmianie w czasie, co utrudnia pomiar.
Ze względu na obecność sygnałów harmonicznych i interharmonicznych, częstotliwość Fouriera, która jest największym wspólnym podzielnikiem dla wszystkich składowych częstotliwości występujących w sygnale, jest różna od podstawowej częstotliwości napięcia zasilającego jest zwykle bardzo mała. Przy tym sposobie analizy musimy uwzględnić dwa rodzaje problemów:
- Minimalny czas próbkowania sygnału jest długi w związku z tym liczba próbek sygnału jest duża.
- Podstawowa częstotliwość Fouriera będąca podstawą pomiaru jest trudna do odnalezienia, ponieważ częstotliwości wszystkich składowych sygnału mierzonego nie są do końca znane.
Można przytoczyć przykład sygnału z zawartością interharmonicznej: sygnał analizowany jako suma trzech składowych, podstawowej (50 Hz) i interharmonicznej (91,2 Hz) i wyższej harmonicznej (2500Hz).
Podstawowa częstotliwość Fouriera w tym przypadku to 0.2 Hz, jest ona dużo mniejsza od częstotliwości podstawowej. Okres tego sygnału to 5 s i w związku z tym minimalny czas próbkowania wynosi 5 s.
Przyjmując częstotliwość próbkowania licznika (stała impulsowania) jako 5000 próbek [2] – najmniejsza potrzebna liczba próbek M jest równa 25 000. W przypadku braku składowej interharmonicznej (91.2 Hz) minimalny czas pomiaru wynosi 20 ms a liczba próbek wynosi 100 [2].
W praktycznych zastosowaniach, ze względu na sprzętowe i softwarowe ograniczenia liczba próbek M nie może być większa niż ustalona wartość maksymalna która może zostać przeliczona przez zaimplementowany układ w liczniku energii elektrycznej. W konsekwencji ograniczany jest czas pomiaru. Przyjęcie czasu pomiaru różnego od podstawowego okresu Fouriera skutkuje nieciągłością pomiędzy sygnałem na początku i końcu okna pomiarowego. Efektem są błędy w identyfikacji okresu składowych, co jest znanym zjawiskiem tzw. przecieku widma.
Przedstawione w tym punkcie zagadnienia dotyczą cyfrowego pomiaru jednej wielkości (np. prądu, napięcia). Problemy pomiaru mocy są jednak bardziej skomplikowane. Częściowo pokazano to w artykule [4].
4. Poprawa niezawodności zasilania – liczniki AMI.
Na jakość i niezawodność dostaw energii wpływają następujące parametry:
- Niezawodność dostawy, rozumiana jako zdolność dostarczania w sposób nieprzerwany wymaganej ilości energii.
- Jakość dostarczanej energii elektrycznej, identyfikowana poprzez takie cechy dostarczanej energii jak: wartość napięcia, częstotliwość, zawartość harmonicznych, asymetria napięcia, migotanie, itp.
- Jakość obsługi odbiorcy, rozumiana jako szybkie przywrócenie zasilania, informowanie o przyczynach wyłączenia itp.
System AMI (rys. 4) pozwala nie tylko na rozliczanie energii elektrycznej ale też na dwukierunkową komunikację z licznikami energii, monitorowanie jakości energii, poprawę niezawodności, możliwość zapobiegania zakłóceniom w przypadku wystąpienia awarii sieci [9,10].
Liczniki komunalne AMI (rys. 5), pozwalają mierzyć parametry jakościowe energii elektrycznej jednak samo pojawienie się przekroczeń dopuszczalnych wartości parametrów jakości energii elektrycznej nie dostarcza żadnych informacji o przyczynach pogorszenia jakości np. napięcia. Przebiegi napięcia są bowiem efektem wzajemnego oddziaływania na siebie źródeł zasilania i odbiorników.
System AMI umożliwia też ciągłe monitorowanie i raportowanie wszelkich odchyleń od zadanych parametrów jakości energii.
Możliwe też jest dostarczanie informacji o ewentualnym nielegalnym poborze energii elektrycznej, co pozwoli na zmniejszenie strat handlowych jak też pozwoli na szybszą reakcję służb OSD.
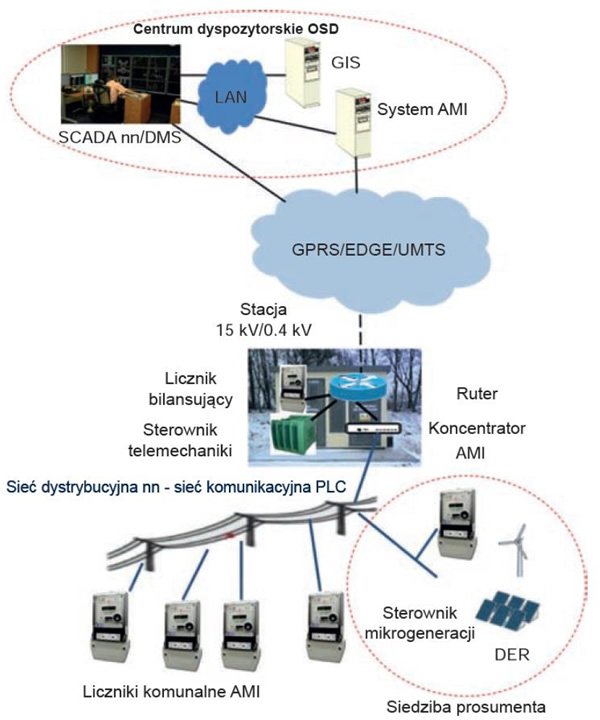
monitorowania i sterowania sieci nn [11]
Liczniki bilansujące AMI montowane w stacjach SN/nn pozwolą na monitorowanie zawartości harmonicznych czy wskaźnika THD, jak też umożliwią zastosowanie ewentualnych środków zaradczych w przypadku stwierdzenia występowania zakłóceń czy awarii sieci zasilającej środków zaradczych w przypadku przekroczenia dopuszczalnych czy zadanych parametrów jakości i niezawodności sieci.

Omówiona w niniejszej publikacji problematyka pomiaru mocy przy przebiegach odkształconych to zaledwie początek szczegółowej analizy, która zostanie przedstawiona w następnych artykułach. Nadmienić należy że ciągłe postępujące szukanie “oszczędności” przez odbiorców energii polegające na montażu “energooszczędnego” oświetlenia (świetlówki kompaktowe, oświetlenie diodowe , zasilacze impulsowe) , coraz bardziej popularne instalowanie mikroźródeł energii (instalacje fotowoltaiczne) powoduje coraz większe generowanie harmonicznych w sieci energetycznej zwłaszcza po stronie niskiego napięcia (przekształtniki , inwertery) stwarza to coraz większe trudności w prawidłowym zliczaniu pobieranej energii elektrycznej przez liczniki statyczne jak tez zachowanie niezawodności zasilania.





























